ヤンマーテクニカルレビュー

Abstract

In order to predict and evaluate the rotary tiller leveling performance, the pile height of soil tilled by the rotary tiller was experimentally measured by a laser range scanner and estimated using the rotary tillage model developed through the discrete element method (DEM). The comparison between the simulated and the experimental results indicated that this model was able to predict the pile shape of tilled soil. Additionally, this model was able to estimate the influence of mechanical specifications (rotary tiller width, rotary tiller blades arrangement and blade shape) on the root-mean-square (RMS) value of pile height distribution after tillage. The determination coefficient of the RMS value was 0.799.

1.はじめに

ロータリ耕うん機の性能には，砕土性，反転性，均平性，稲藁のすき込み性，所要動力等様々なものが挙げられるが，本報告では均平性能に焦点を当てた。ロータリ耕うん機の均平性能は，後工程の播種・移植等の作業精度を左右し，作物の初期生育に影響を及ぼす非常に重要な性能である。ロータリ耕うん機の均平性能に対する機械設計パラメータ（耕うん幅，耕うん爪配列，耕うん爪形状等）の影響をコンピュータによるシミュレーションで予測することができれば，設計および性能評価にかかる時間と労力が大幅に低減され，非常に意義が大きい。

本報告では，個別要素法⁽¹⁾を用いて先行研究^(2),(3)にて構築したロータリ耕うんモデル（図1）を用いて耕うん後の土壌の堆積形状を予測し，均平性能の評価を試みた。機械設計パラメータの均平性能への影響を明らかにするため，仕様の異なる2種類のロータリ耕うん機で圃場試験を実施した。耕うん後の土壌の堆積形状をレーザ式測域センサで計測し，ロータリ耕うんモデルの計算結果と実測結果を比較した。そして，耕うん後の土壌の堆積高さの二乗平均平方根に対する機械設計パラメータおよび運転条件（PTO速度段，走行速度）の影響についても，ロータリ耕うんモデルの計算結果を実測結果と比較検証した。

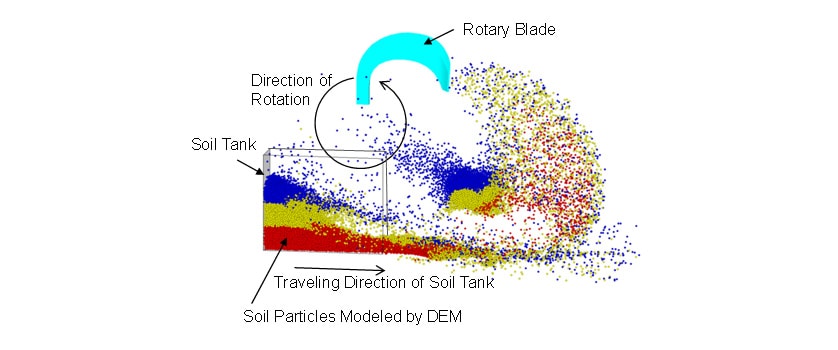
2.方法

2.1.均平性能の評価試験方法

ロータリ耕うん機の均平性能は，リアカバーを全開にした状態で耕うんを行い，土壌の堆積形状の高低差や山の形で評価した。ロータリ耕うん機の均平性能評価試験の様子を図2に示す。試験では仕様の異なる2種類のロータリ耕うん機を供試した。供試機Aの耕うん幅は2.0m，耕うん爪の本数は44本である。供試機Bの耕うん幅は1.7m，耕うん爪の本数は36本である。供試機AおよびBは，ともにサイドドライブ型のダウンカットタイプである。供試機AとBの耕うん爪の主要寸法を表1に示す。どちらの耕うん機も“なたづめ”と呼ばれるC型の耕うん爪を装備している。

表1 Principal dimension of tested rotary blades

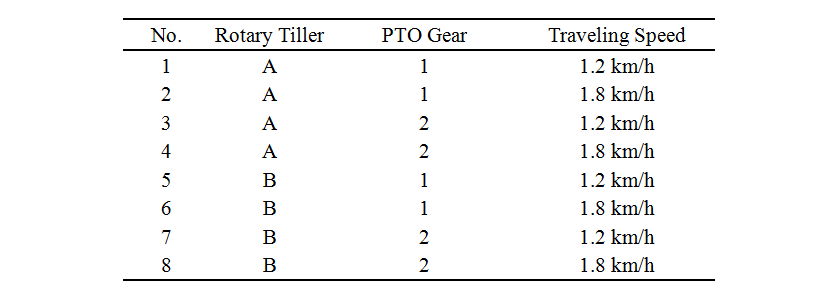
試験条件を表2に示す。試験ではロータリ耕うん機の耕深を一定に保つため，尾輪を用いて耕深14cmに設定した。ロータリ耕うん機2型式，トラクタのPTO速度段2水準，走行速度2水準とし，計8条件の試験を実施した。なお，供試したトラクタのPTOの1速は544rpm，2速は761rpmである。

表2 Test conditions

ロータリ耕うん機の均平性能は，土壌の堆積形状の高低差が小さく，耕うん幅方向に大きな凹凸が無いことが望ましい⁽⁴⁾。本報告では，耕うん後の土壌の堆積高さの二乗平均平方根を均平性能の評価指標として用いた。土壌の堆積形状はレーザ式測域センサ（北陽電機，UGR-04LX）を用いて上方から凹凸の高さ方向の値を計測した。用いた計測器（図3）は，高さ1.0m，幅1.5m～2.2mに調整可能なアルミフレームの中央の上部にレーザ式測域センサを備え，データ記録用のノートPCおよびセンサ用の電源を装備している。アルミフレームの上部には水準器を設け，レーザ式測域センサを水平に配置した。各試験条件で耕うんを行った後，土壌の堆積形状をロータリ耕うん機の走行方向30cm間隔で5断面を記録した。本計測器の場合，計測した地表面の凹凸はセンサ中心から約0.36°（360°/1024分割）ごとのデータとして記録されるため，耕うん幅方向1cmの等間隔のデータへ線形補間し，5断面の平均値を求めた。

2.2.土壌の堆積形状の予測方法

耕うん後の土壌の堆積形状は，先行研究で構築したロータリ耕うんモデル（図1）を用いて予測した。ロータリ耕うんモデルに適用したパラメータ（土粒子の直径，密度，摩擦係数，ばね定数，減衰比，計算時間間隔）およびモデル化手法は文献⁽²⁾と同様とした。計算条件は均平性能の評価試験の試験条件（表2）と同様に8条件とした。耕深は14cmに設定した。ロータリ耕うんモデルの耕うん軸回転数は，供試したトラクタのPTO軸の回転数とロータリ耕うん機の駆動ギアの減速比から計算し，PTO速度段1速の場合は184rpmに，2速の場合は258rpmに設定した。

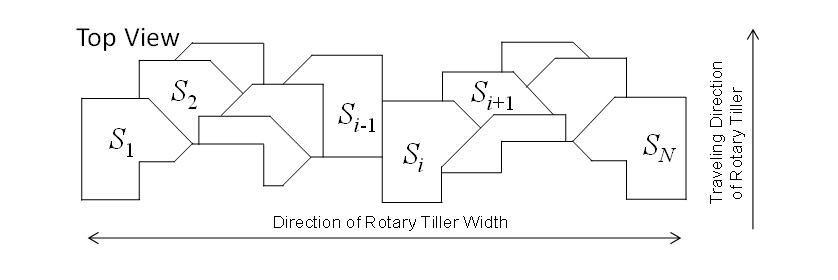
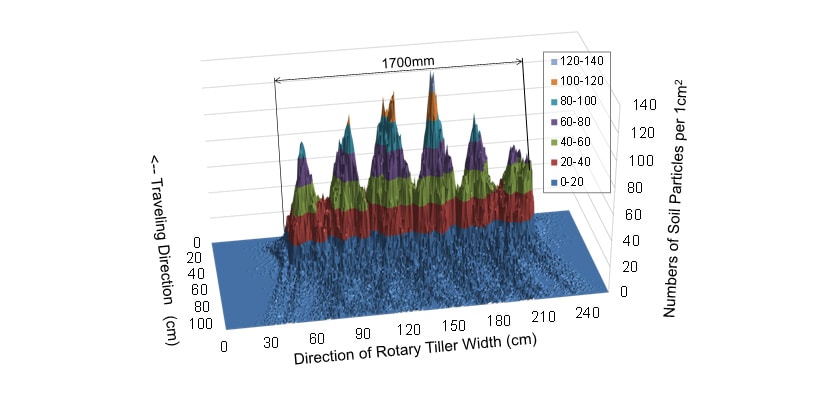
耕うん後の土壌の堆積形状を予測するための概念図を図4に示す。本報告では，耕うん幅の土壌の堆積高さの平均値をゼロとし，鉛直上方をプラス方向と定義した。耕うん後の堆積形状を予測するための土粒子数の分布は，ロータリ耕うんモデルで計算した耕うん爪1本当たりの土粒子数の分布を重ね合わせて算出した。ロータリ耕うん爪1本当たりの土粒子数の分布の一例を図5に示す。ここで，耕うん爪で耕うんされる土粒子数は，圃場表面のロータリ耕うん機切削パターン（図6）の耕うん爪各々の切削面積に依存すると仮定した。図6中に示した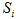は，耕うん爪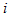の圃場表面の切削面積である。ロータリ耕うん機切削パターンは，ロータリ耕うん機の機種ごと，試験条件ごとに算出した。

ロータリ耕うん機で耕うんされた土粒子数の分布は，式(1)で算出した。

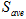ここで，は耕うん爪の本数，は耕うん爪全ての切削面積の平均値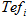，はトラクタ後輪で形成される轍（わだち）による影響を考慮するための補正係数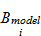，はロータリ耕うんモデルで計算された耕うん爪 の土粒子数の分布である。と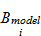は両者ともに120行×255列の行列であり，どちらも単位面積（1cm²）当たりの粒子数分布である。行列の行がロータリ耕うん機の走行方向，列が耕うん幅方向に対応する。ここで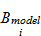は式(2)に示すように，図4の100行×50列の粒子数分布（式(2)中の破線で囲まれた領域に対応する）をロータリ耕うん機の走行方向および耕うん幅方向に耕うん爪配列に従って，耕うん爪の湾曲方向（右向きもしくは左向き）ごと，耕うん爪ごとに移動させた行列である。

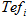の値は式(3)を用いて定義した。

ここで，はロータリ耕うん機の耕深を表し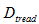，はトラクタ後輪で形成される轍の深さである。トラクタ後輪の後方に位置する耕うん爪は，形成された轍の分だけ耕うんする土が少なくなると仮定した。均平性能の評価試験時の観察結果から，ロータリ耕うん機の耕深は14cm，轍の深さ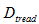は8cmであったため，補正係数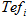は轍の影響を受ける耕うん爪は0.4286，影響を受けない耕うん爪は1.0の値をそれぞれ用いた。モデルの堆積高さは，土粒子数の分布を耕うん方向に平均し，単位面積当たりの土粒子の数と土粒子の体積から算出した。

3.結果と考察

3.1.耕うん後の土壌の堆積形状

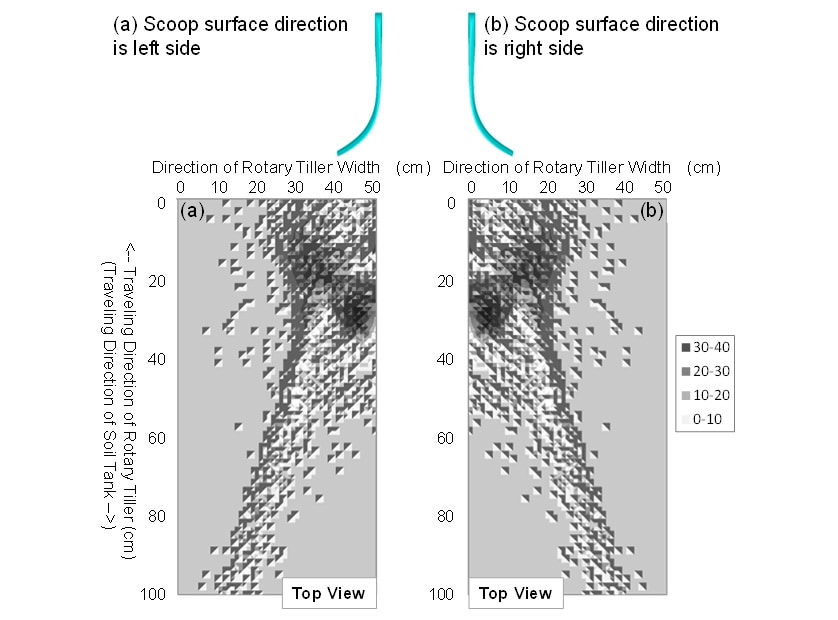
耕うん後の土壌の堆積形状を予測するため，ロータリ耕うんモデルを用いて耕うん後の土粒子分布を試験条件ごとに算出した。供試機AとBの耕うん後の土粒子数の分布を図7と図8にそれぞれ示す。試験条件はPTO速度段1速，走行速度1.2 km/hである。結果より，ロータリAで耕うんされた土粒子の分布形状はロータリBのものよりも山の高さが高いことが分かる。そして，どちらの分布形状も6つの小さな山が形成されていることが分かる。図7および図8と同条件のロータリ耕うん機の均平性能評価試験後の土壌の堆積形状の様子を図9に示す。図9中にはレーザ式測域センサで計測した土壌の堆積形状を重ねて示した。実測した土壌の堆積形状とモデルの予測結果を比較すると，モデルで算出した土粒子の分布形状が圃場試験で実測した耕うん後の堆積形状と山の形と数が似通っていることが分かる。

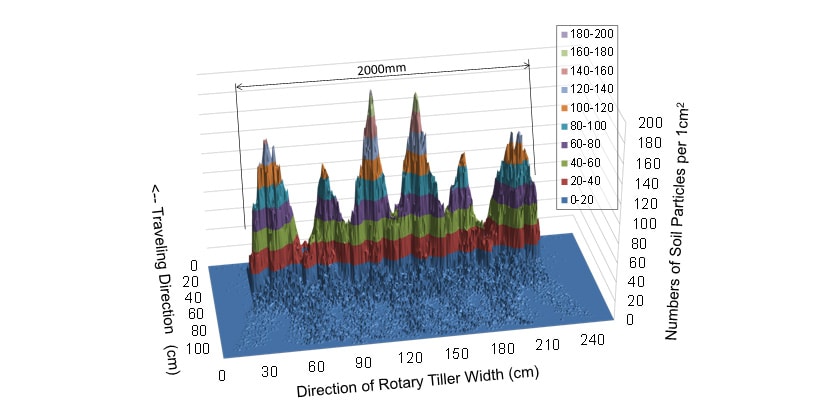
モデルの予測結果の妥当性を定量的に評価するため，耕うん後の土壌の堆積高さのモデルの計算値と実測値をロータリ耕うん機の機種ごとに図10で比較した。試験条件は図7，図8および図9と同様，PTO速度段1速，走行速度1.2km/hである。堆積高さの実測値と計算値の比較から，ロータリAでは両端の山の幅が実測値の方が計算値よりも広く，4つの山とも見て取れるが，ロータリAとBの両者で6つの小さな山が形成されており，その形状と高さが概ね似ていることが分かる。ロータリAの場合，堆積高さの高低差の最大値は計算値が67.2mm，実測値が53.8mmであり，計算値が実測値の124.9%であった。ロータリBの場合，堆積高さの高低差の最大値は計算値が46.5mm，実測値が34.7mmであり，計算値が実測値の134.3%であった。結果から，実測値と計算値共に，ロータリAの耕うん後の土壌の堆積高さの高低差の最大値がロータリBのものよりも高く，ロータリ耕うんモデルは耕うん後の土壌の堆積形状と高さを予測できる可能性が示唆された。

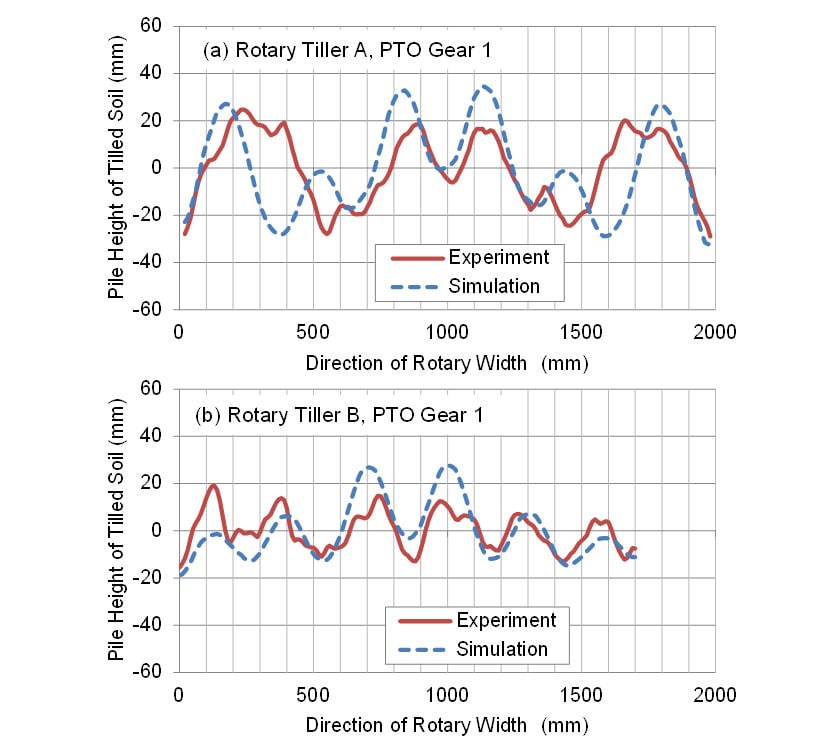
PTO速度段が2速の場合の土壌の堆積高さをロータリ耕うん機の機種ごとに実測値と計算値で比較した結果を図11に示す。図11(a)中に示すように，ロータリAの場合，土壌の堆積高さは計算値が実測値と異なっている。これは，均平性能評価試験時にロータリ耕うん機が傾いたことが影響したものと推察した。一方，ロータリBの場合（図11(b)），堆積形状の計算値は実測値と傾向が良く似ていることが分かる。堆積高さの高低差の最大値は計算値が31.3mm，実測値が26.9mmであり，計算値が実測値の116.7%であった。また，ロータリAの堆積高さの高低差の最大値はロータリBよりも実測値と計算値共に高くなる結果を示した。この傾向はPTO速度段1速の結果（図10）と同様であった。

ロータリAとBの機械設計パラメータ（耕うん幅・耕うん爪配列・耕うん爪形状）は全て異なり，本報告で提案した土壌の堆積形状の予測方法は，これら機械設計パラメータの影響を考慮したものである。PTO速度段1速および2速のどちらの場合にも，ロータリAの堆積高さがロータリBよりも実測値と計算値共に高くなった結果から，本報告で示した予測手法は，耕うん後の堆積形状に対する機械設計パラメータ（耕うん幅，耕うん爪配列，耕うん爪形状）の影響を予測できる可能性が高いと言える。

3.2.土壌の堆積高さの二乗平均平方根

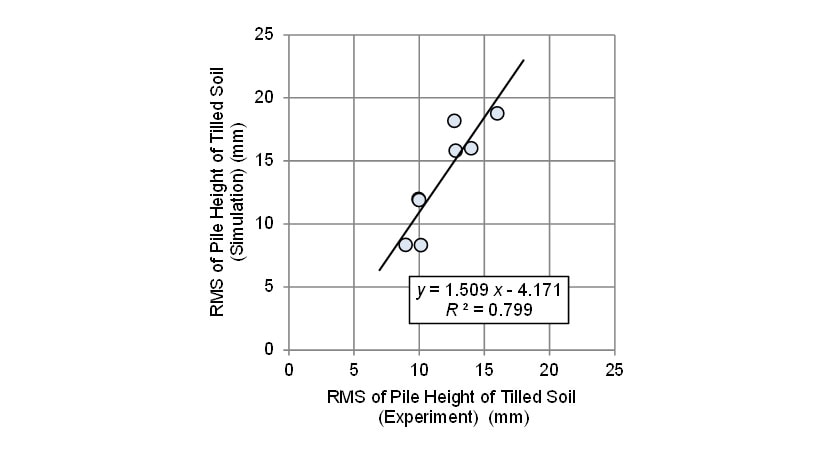
耕うん後の土壌の堆積高さの二乗平均平方根を計算値と実測値について，全ての試験条件で比較した結果を図12に示す。実測値と計算値の近似直線の傾きは1.509，決定係数は0.799であった。堆積高さの二乗平均平方根の計算値は実測値よりも平均で15.6%高い値を示した。この傾向について2点考えられる。一つ目の理由は，ロータリ耕うんモデルで耕うんされた土粒子は地面に接触した時点で粒子の数を計上し積み重ねたため，実現象のように土粒子が崩れ安定するところまでモデルで考慮できていないためである。第二の理由として，一度耕うんされ投てきされたモデルの土粒子は空中で他の耕うん爪に再度接触しないが，実際のロータリ耕うん機の内部では，土壌は他の爪で跳ね返るためと考えられる。ロータリ耕うん後の土壌の堆積形状の予測精度を更に向上させるためには，耕うん爪による土粒子の跳ね返りを考慮したうえ，土粒子が崩れ安定するまでモデルで計算する方策が有効である。他の方策としては，ロータリ耕うん機全体をモデル化するような大規模なモデルを用いて計算する手法も考えらえる。しかし，精度向上のためモデルの規模が大きくなると，計算にかかる時間が膨大になるため，求める予測精度とかかる労力のバランスを見てモデル化手法を選択することが肝要である。

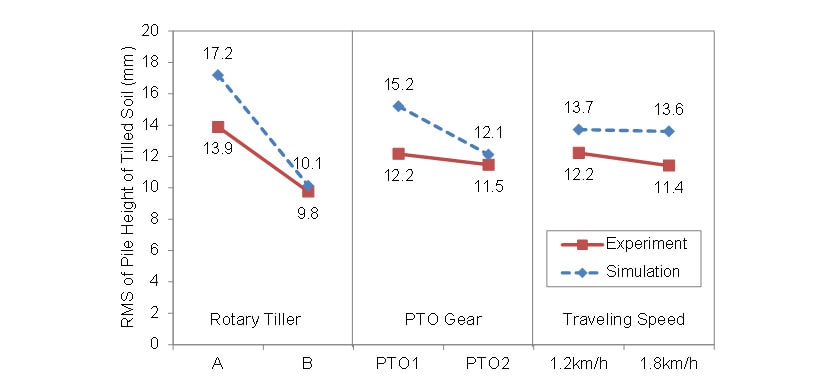
均平性能に対する機械設計パラメータと運転条件（ロータリ耕うん機，PTO速度段，走行速度）の影響を定量評価するため，耕うん後の土壌の堆積高さの二乗平均平方根に対する各因子の分散分析を実施した。各因子の主効果を計算値と実測値で比較した結果を図13に示す。各因子の主効果は計算値が（ロータリ耕うん機）>（PTO速度段）>（走行速度）の順であり，実測値が（ロータリ耕うん機）>（PTO速度段）≒（走行速度）であった。これらの結果から，計算値と実測値の両者で二乗平均平方根に対する機械設計パラメータ（ロータリ耕うん機）の影響が運転条件（PTO速度段と走行速度）よりも大きく，本モデルを用いてロータリ耕うん機の均平性能に対する機械設計パラメータ（耕うん幅，耕うん爪配列，耕うん爪形状）の影響を設計段階で予測することが可能と言える。

4.おわりに

ロータリ耕うん機の均平性能を予測し評価するため，ロータリ耕うんモデルを用いて耕うん後の土壌の堆積形状を予測した。機械設計パラメータの均平性能への影響を明らかにするため，仕様の異なる2種類のロータリ耕うん機で圃場試験を実施した。耕うん後の土壌の堆積形状をレーザ式測域センサで計測し，ロータリ耕うんモデルの計算結果と実測結果を比較し，以下の知見を得た。

• (1)ロータリ耕うんモデルを用いて耕うん後の堆積形状の山の数と高さを予測できる可能性が示された。
• (2)ロータリ耕うんモデルは，耕うん後の堆積高さ，均平性に対するロータリ耕うん機の機械設計パラメータ（耕うん幅，耕うん爪配列，耕うん爪形状）の影響を設計段階で予測できる。
• (3)堆積高さの二乗平均平方根の計算値と実測値の決定係数は0.799であった。

文献

• (1)Cundall, P. A., Strack, O. D. L., A discrete numerical model for granular assemblies. Geotechnique, 29(1), 47-65, 1979.
• (2)平澤一暁，片岡　崇，丹生秀和，久保孝之，ロータリ耕うんの動的現象の解析研究（第1報）―土の投てきと耕うん軸トルクのモデル化―. 農業機械学会誌，75(5), 307-315, 2013.
• (3)平澤一暁，片岡　崇，丹生秀和，久保孝之，ロータリ耕うんの動的現象の解析研究（第2報）―爪形状の土の投てきと耕うん軸トルクへの影響―. 農業食料工学会誌, 76(1), P55-61, 2014.
• (4)坂井　純, 柴田安雄, トラクタ用ロータリ耕なた刃の配列設計理論. 農業機械学会誌, 40(1), 29-40, 1978.